One of the simplest geometric
paradoxes with vanishing areas was described by Martin
Gardner in his classic book, Mathematics, Magic and
Mystery, (1956).1 The paradox is more
than two centuries old, but it still attracts attention
of puzzlers, mathematicians, and magicians. And that is
why there are dozens of different variations based on its
principle.
-----
Important:
All puzzles are published here with the kind permission
of their authors, where applicable. Copyright to all
presented puzzles stays with their respective
authors, unless otherwise is stated.
----- |
|
|
|
 |
Printable Puzzle: To
solve some of the puzzles which will be described below
you can print their pieces. For this, click the
respective image marked with the "pp" pictogram
(as that shown at left) to go to a new window with the
puzzle tiles; then you can print them and cut them out. |
|
 |
Copyright Note: Note
that all presented puzzles are copyrighted, so you can
print them for your own use only, and not for any kind
of commercial profit. |
|
|
 |
Play Puzzle: Click
an image marked with the "pp" pictogram (as that
shown at left) to go to a page with an interactive
version of the respective puzzle. |
|
|
|
|
|
|
The Holey Square |
The basic idea is that a square is
dissected into four pieces so that they can be
reassembled into another square with seemingly the same
sizes, but with a square hole in it.
|



|
The Holey Square without
and with a hole in it. The sample was hand-crafted by
the author in the early
70's.
|
|
|
There are many versions of this
puzzle-paradox based on the described principle, but with
improved pieces. Some versions use a rectangle instead
of a square; among them several versions exploit a
playing card theme, while some other use an internal
rectangular piece with some pictures, inscriptions, or
even as... a business card(!). Also, there are clever,
3D versions of this classic puzzle-paradox. Using an
asymmetric pattern for dividing a plain square, we can
make amazingly tricky puzzle-paradoxes. The simplest of
them is described just below.
|
|
|
|
The Coin Puzzle-Paradox |
|
by
Serhiy Grabarchuk |
Four quadrilateral pieces with
coins pasted on both of their sides make a square with a
hole in the middle. One more coin is placed within the
hole. If you will take that coin away, the four
remaining ones make a square with a free square hole
within. Now, you can rearrange the four pieces so that
big square appears again. And again four coins make the
same square of the same size and in the same orientation
as in the initial pattern, but now no hole remains
anymore. How can that be possible?
|
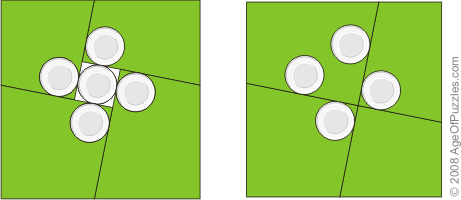 
|
The square with five coins
and a hole, and the new square with four coins and no
hole in it.
|
You can prepare the pieces to
perform the trick. For this click the above image to
open the unfolded patterns of the pieces, print them,
cut them out, fold four of them along the dotted lines
in half,
and use some glue to join the halves in each piece
together.
|
|
|
|
|
|
Where Is the 5?2 |
|
by
Serhiy Grabarchuk |
It is a simple trick with four quadrilaterals. They make up a square with a traditional magic square,
3 x 3 on it; its magic constant is 15, what means that
each of its rows, columns, and both main diagonals add
up to 15. When you shuffle the pieces, and then flip
them over, you will see fragments of another, 3 x 3
magic square. Restore it and you will see how one of the
numbers disappears... To learn more click the thumbnail
just at left.
|
|
|
|
|
|
|
|
A Holey Number3 |
|
by Werner Miller |
This puzzle-paradox is just similar to the above
described trick, and combines a holey square and a 4 x 4
pandiagonal magic square. The four quadrilateral pieces
with printed numbers 0 through 15 are assembled into a
square with a 4 x 4 magic square on it; each of its
rows, columns, and both main diagonals add up to 30.
Then pieces are flipped over, and again they can produce
a magic square with the same magic constant 30, although
now the whole square 4 x 4 lacks one cell. Is not that
odd?... Click the thumbnail just at left to learn more.
|
|
|
|
|
|
Puzzle-Paradox Mosaic |
|
by
Serhiy Grabarchuk |
This Tangram-like set is based on
the Holey Square's pattern with each of its
quadrilaterals divided into two different right
triangles--an isosceles triangle, and a triangle in the
size of a half-domino. Note that the area of the full
square is 10, and so its side is sqrt10. Using the full
set every time, we can form two different squares (with sides 1 and
3); two equal squares (with sides sqrt5); different sets
of three and four squares; and a lot of different
shapes. You can flip pieces over, but not overlap.
|
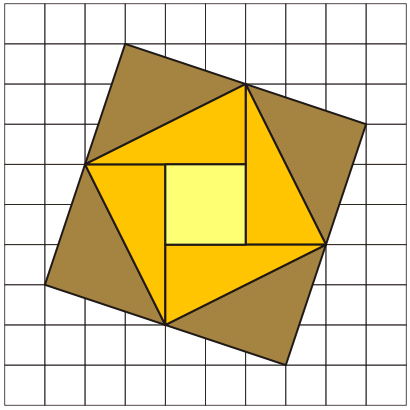 
|
The Puzzle-Paradox Mosaic
consists of nine pieces: eight right triangles of two
different kinds, and a single square.
|
|
|
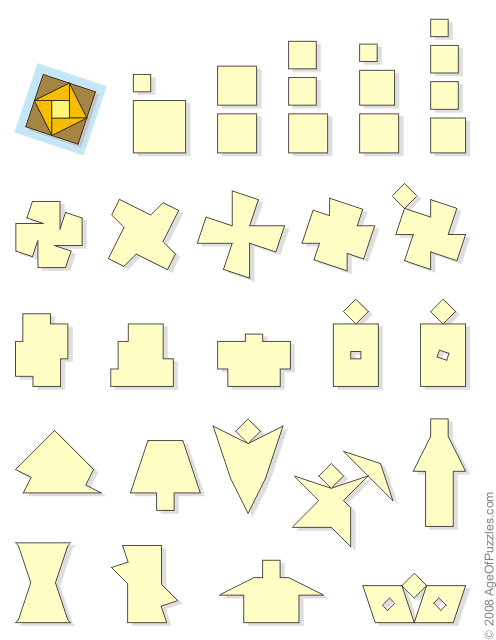
|
Assemble these shapes, using
all the nine pieces of the Puzzle-Paradox Mosaic.
|
