 |
| |
A Colorful Journey through Endless Patterns of Quick Wits |
|
|
|
|
|
|
|
|
|
Home
/
Publications /
Seven
Puzzles for G4G7 |
|
|
|
|
|
|
The
Gathering for Gardner (G4G) is the unique biennial
event founded in 1993 by Gardner fan and puzzle
collector, Tom Rodgers. Many enthusiastic and talented
folks are organizing it in Atlanta every second year,
and the World's foremost mathematicians, puzzlers and
magicians, deeply influenced by Martin Gardner's work
and life, are attending G4G's.
Gathering in Atlanta, each G4G participant brings with
him/her some writings related to math, magic, or
puzzling, and prepared specially to honor Martin
Gardner. Then these pieces are exchanged between all G4G
participants. The seven different puzzles below are my
Exchange Gift for G4G7.
----- |
|
 |
Printable Puzzle: To
solve some of the puzzles which will be described below you
can print their pieces/grids. For this, click the respective
image marked with the "pp" pictogram (as that shown at left) to go to a new window with the puzzle pieces/grids; then you
can print them and (when necessary) cut them out. Note that all these puzzles
are copyrighted, so you can print them for your own use only,
and not for any kind of commercial profit. |
|
 |
Play Puzzle: Click
an image marked with the pictogram shown at left to go
to a page with an interactive version of the respective
puzzle. |
|
|
|
|
|
|
Puzzle I |
|
|
|
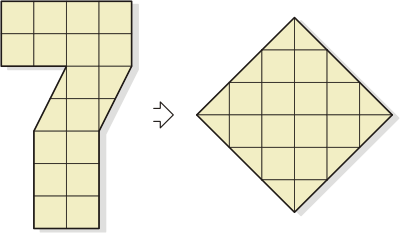
Squaring the Seven |
Divide the Seven shown below into
five parts and rearrange them into a square as that
shown in the illustration. The grids within the Seven
and square are provided just for the purpose of showing
the exact proportions of its elements, so you can use
the grids’ lines as you will wish, but the Seven’s area
has to be fully used. Pieces can be rotated and turned
over, but not overlapped.
|
|
Divide the Seven into five
parts so that to rearrange them into a square..
|
|
|
|
Puzzle II |
|
|
|
Seven Stars |
With three straight lines divide
the Seven shown below into seven parts so that each part
contains a single star. Find two substantially different
solutions.
|
 
|
Divide the Seven into seven
parts with a single star each.
|
|
|
|
|
|
Puzzle III |
|
|
|
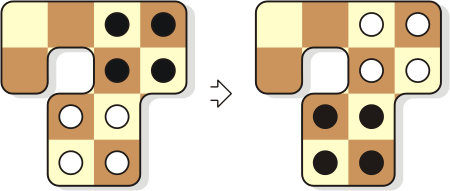
The Coin Seven Challenge |
The Seven shown below at left is
assembled of six coins. Light and dark circles represent
different sides of coins. Moving one coin at a time,
exchange coins in the Seven exactly as shown below, in
the right diagram. Could you achieve this in five
single moves? Important. To ensure an exact
position for each coin after its move, it must touch to
at least two coins from the unmoved group. But remember
that there is one illegal move when you simply move a
coin between two other ones so that all the three coins
form a straight line.
|

|
In five single moves invert
the Seven's pattern.
|
|
|
|
Puzzle IV |
|
|
|
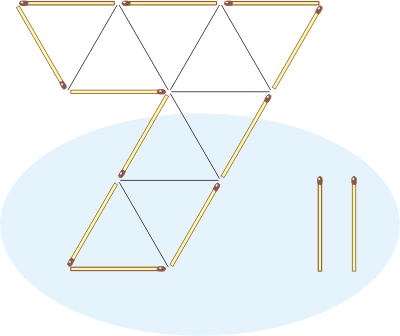
Halving the Match Seven |
Using two matchsticks, divide the
Seven shown in the illustration below into two parts of
the same area. The lines within the Seven are provided
just to show its exact proportions. Note that
matchsticks in the puzzle are used as math segments of
length 1, and each matchstick must be used with all its
length, so no loose ends of matchsticks should be
formed. Matchsticks must not overlap each other, and you
are not allowed to break and/or bend them.
|
|
With two matchsticks divide
the Match Seven into two parts of the same area.
|
|
|
|
Puzzle V |
|
|
|
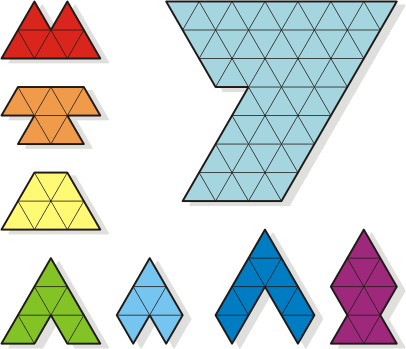
The Seven Fish Seven |
Using all the seven fish shown in
the illustration below, form the Seven presented just
next to them. Pieces can be rotated, but not overlapped
and/or overturned.
|
|
Using all the seven fish,
form the Seven shape.
|
|
|
|
Puzzle VI |
|
|
|
The Origami Seven |
You have a square piece of paper
colored on one of its sides and white on the other; it
is a so-called Origami square. The challenge is to fold
it exactly seven times so that to get a smaller, flat
square with the Seven within it exactly as presented
below in the right diagram.
You are allowed to fold one or several layers of paper
at a time, counting this as a single fold; such a simple
fold is called a “book fold." Thus, the final square may
have several layers of paper in any of its points. Each
plain color element of the square may be either a really
plain color surface, or consist of several one-colored
parts. It is true about each white part as well.
The dotted lines on the Seven are provided just for the
purpose of showing its exact proportions; it is obvious
that the Seven is inscribed within a 3x3 grid. Note that
the back side of the final square may have any pattern.
Also, bear in mind that the shown mutual sizes of the
starting Origami square and the final square with the
Seven are relative.
You can mark and pre-crease all necessary lines to folds
using some additional tools, but before you start to
fold the Origami square and counting folds, it must be fully
unfolded and flat.
|

|
In exactly seven simple
folds get the Origami Seven.
|
|
|
|
Puzzle VII |
|
|
|
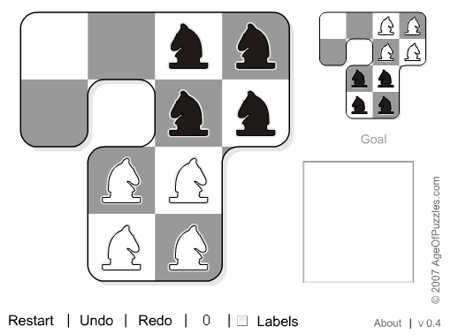
Eight Knights in the Seven |
Eight chess knights -- four white
and four black ones represented by small circles -- are
placed on the 7-like chessboard as shown in the left
diagram below.
Now, performing just normal knight’s moves from cell to
cell of the chessboard, exchange the white and black
knights as shown in the right diagram below.
Can you exchange the knights in exactly twelve moves,
counting a consecutive series of leaps of a knight as
one move? Hint. To achieve this goal you should perform
moves by knights of different colors alternately.
To solve the puzzle you can use eight small coins placed
directly on a big board; to get to it, click any of the
challenge diagrams just below.
|
|
Exchange the white and
black knights in exactly twelve knight's moves.
|
|
|
Also, you can go to our page with
the
interactive Flash version of the puzzle. You can
also click the image just beneath.
|
|
Play our interactive Flash
version of the puzzle.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Last Updated:
July 3, 2011
Posted: May 28, 2006 |
|
|
|
|
|
|
|
|
|
