|
|
 |
An Origami square.
|
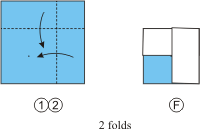 |
How to get a 2x2 checkered pattern.
|
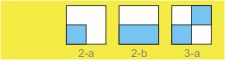 |
Three 2x2 checkered patterns.
|
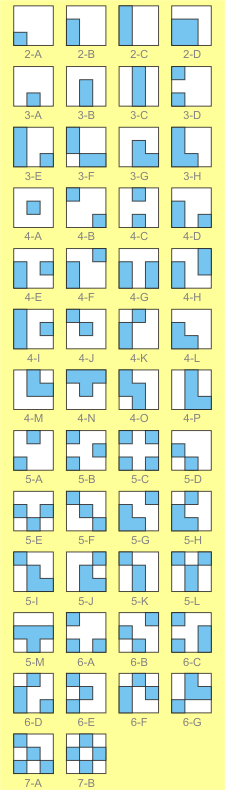 |
Fifty 3x3 checkered patterns.
|
|
|
|
|
The object is simple: Take a square sheet of paper
(colored at one side, and white on the other), and
performing just "book folds" get a checkered pattern in
the minimal number of single folds. No matter what
pattern will be at the back of every final packet.
A small sample at left shows how to get a 2x2 square
pattern with one colored cell.
In fact, you have three patterns 2x2, and fifty patterns
3x3 to play with; they are shown in the diagrams in this
page. Numbers next to them indicate the minimal folds
necessary to perform them.
The patterns were devised, solved, improved, and
popularized by the following puzzle folks: Nob
Yoshigahara, Koji Kitajima, Hiroshi Yamamoto, Setsuo
Sasaki, Andy Liu, Tom Hull, Keiichiro Ishino, and the
author.
Write
us if you can improve any of these results.
***
Much more difficult challenges can be finding all the
4x4 checkered patterns and, then, finding their minimal
solutions. Recently, Keiichiro Ishino calculated that
there are 5,038 substantially different 4x4 checkered
squares. Part of them have their solutions quite similar
to the respective 3x3 checkered squares described here,
but it is obvious that most of them are rather difficult
to be optimized. |
|
|
|
|
