|
|
 |
An Origami triangle.
|
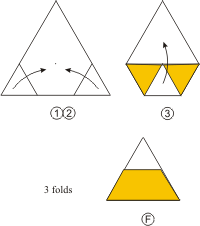 |
How to get a 2-unit-side checkered
triangle.
|
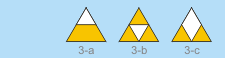 |
Three 2-unit-side checkered
triangles.
|
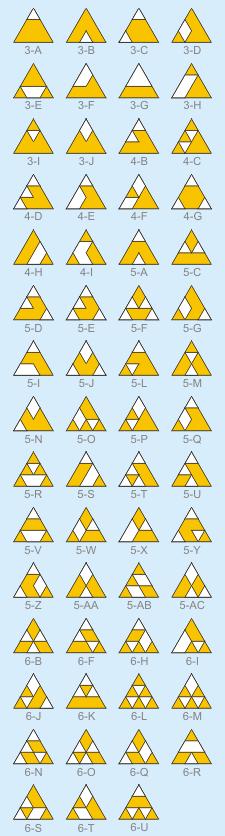 |
Fifty-nine 3-unit-side checkered
triangles.
|
|
|
|
|
This is a triangular version of the Origami Checkerboard
puzzle. It is also a rare triangular Origami work since
it uses a sheet of paper in the form of an equilateral
triangle colored just on one of its sides.
A small sample at left shows how to get a 2-unit-side
triangle with one colored cell.
In this page you can see three, 2-unit-side patterns,
and fifty-nine 3-unit-side patterns. Your challenge is
to achieve every of the proposed patterns in the minimum
of single "book" folds. The final shape every time is a
flat equilateral triangle; no matter what pattern will
be at its back. Numbers next to the patterns indicate
the minimal known numbers of folds necessary to perform
them.
Write us if you can improve any of these results.
Pattern 6-U, solution to it, and solutions to patterns
3-c, 4-I, 5-W, 5-X, 5-Y, 5-Z, 5-AB, 5-AC, 6-L, 6-M, 6-N,
6-O, 6-Q, 6-R, 6-S, and 6-T were found by Keiichiro
Ishino. A solution to pattern 5-AA was found
independently by Setsuo Sasaki and Keiichiro Ishino.
Solutions to patterns 3-b and 3-J were found by Hirokazu
Iwasawa and Naoaki Takashima, respectively.
***
Much more difficult challenges can be finding all the
4-unit-side checkered triangles and, then, finding their
minimal solutions. Recently, Keiichiro Ishino calculated
that there are 6,605 substantially different 4-unit-side
checkered triangles. Part of them have their solutions
quite similar to the respective 3-unit-side checkered
triangles described here, but it is obvious that most of
them are rather difficult to be optimized. |
|
|
|
|
